Difference between revisions of "Developing Methods to Study Complex Food Webs"
(Created page with "'''Student Researcher:''' Benjamin Barros '''Mentor:''' [http://www.marquette.edu/mscs/facstaff-factor.shtml Dr. Kim Factor] Theoretically, food web...") |
|||
| Line 3: | Line 3: | ||
'''Mentor:''' [http://www.marquette.edu/mscs/facstaff-factor.shtml Dr. Kim Factor] | '''Mentor:''' [http://www.marquette.edu/mscs/facstaff-factor.shtml Dr. Kim Factor] | ||
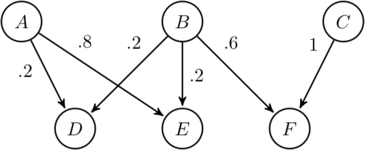
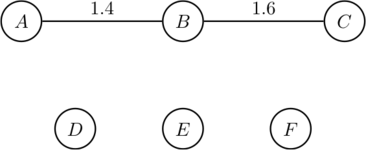
| − | Theoretically, food webs are an effective way to model ecosystems, but in application food webs are often extremely complex. In an effort to understand the food web of a native Hawaiian ecosystem, we define several new types of graphs to help with the study of ecosystems. A graph is a set of vertices (points) and edges (lines) that represent a relationship between two vertices. Competition graphs and (1,2)-step competition graphs show predator and prey relationships. Based on these structures, weights are added to the arcs (directed edges) and edges of different types of directed graphs and graphs. The introduction of weighted arcs and edges allows for empirical data to be used while working with these types of graphs. We also define a directed graph called the benefit digraph that allows us to study the relationship between species that strictly (1,2)-compete. The ultimate goal is to obtain tools that better measure population changes in an ecosystem. | + | Theoretically, food webs are an effective way to model ecosystems, but in application food webs are often extremely complex. In an effort to understand the food web of a native Hawaiian ecosystem, we define several new types of graphs to help with the study of ecosystems. A graph is a set of vertices (points) and edges (lines) that represent a relationship between two vertices. Competition graphs and (1,2)-step competition graphs show predator and prey relationships. Based on these structures, weights are added to the arcs (directed edges) and edges of different types of directed graphs and graphs. The introduction of weighted arcs and edges allows for empirical data to be used while working with these types of graphs (see Figures 1 and 2). We also define a directed graph called the benefit digraph that allows us to study the relationship between species that strictly (1,2)-compete. The ultimate goal is to obtain tools that better measure population changes in an ecosystem. |
| + | |||
| + | {|style="margin: 0 auto;" | ||
| + | | [[File:WeightedFoodWeb.png|frame|x150px|upright|alt=Weighted Food Web|Figure 1: Weighted Food Web]] | ||
| + | | [[File:WeightedPred.png|frame|x150px|upright|alt=Weighted Predator Overlap Graph|Figure 2: Weighted Predator Overlap Graph]] | ||
| + | |} | ||
Revision as of 21:15, 11 August 2015
Student Researcher: Benjamin Barros
Mentor: Dr. Kim Factor
Theoretically, food webs are an effective way to model ecosystems, but in application food webs are often extremely complex. In an effort to understand the food web of a native Hawaiian ecosystem, we define several new types of graphs to help with the study of ecosystems. A graph is a set of vertices (points) and edges (lines) that represent a relationship between two vertices. Competition graphs and (1,2)-step competition graphs show predator and prey relationships. Based on these structures, weights are added to the arcs (directed edges) and edges of different types of directed graphs and graphs. The introduction of weighted arcs and edges allows for empirical data to be used while working with these types of graphs (see Figures 1 and 2). We also define a directed graph called the benefit digraph that allows us to study the relationship between species that strictly (1,2)-compete. The ultimate goal is to obtain tools that better measure population changes in an ecosystem.