User:Schwennesen

Week 1

Wednesday, 01 June 2022

This morning started with a meeting hosted by Dr. Brylow about good research practices and the importance of keeping a daily log. Both and after that, I was reading some literature that my mentor Dr. Puri had sent over. The original project that I was assigned was to use ICESAT-2 data to build a model for predicting sea ice thickness. This project was already started by a different REU student from a previous year [1] and Dr. Puri mentioned a different project, using either locality sensitive hashing and / or quantization methods to approximate nearest neighbor searches for geometry and shapes.

This new project is more appealing to me, in part because it is based on topics that I am already familiar with such as Jaccard Similarity and many notions from set theory and text mining that I have learned about at Michigan Tech. Dr. Puri sent me some preliminary literature including a chapter from what I believe is a textbook on using locality sensitive hashing to compute approximately nearest neighbors for text documents, which is a well studied problem and not the focus of this research project.

The Jaccard Similarity is a measure of the likeness between sets, but it can also be defined for areas such as polygons. For a set it is defined as

Jaccard(A, B) = |A ∩ B| / |A ∪ B|

And for polygons, we do the analogous steps and take the area of the intersection or overlap and divide it by the area of the union or the total footprint of the two polygons put together.

For large datasets, we may be interested in similar objects, but for a dataset with n objects where would be C(n,2) pairs to evaluate with is at least an O(n^2) operation before adding the time needed to compute the Jaccard coefficient. The idea behind locality sensitive hashing (LSH) is to create some hash function h which is more likely to place similar items together and less likely to place dissimilar items together. Most of this information is in [2], and I should find more information about the source of this PDF that Dr. Puri sent me. He also send [3], a shorter paper that he wrote about the principles of using LSH on GIS data and some comparison to other approximate nearest neighbor (ANN) approaches.

Using the references on [3], I have found PDF copies of the remaining references below and will be reading and annotating them in the coming days. In addition to the literature review, I also need to establish the actual research question of interest here and set my sights on a realizable goal for the end of the REU. Currently, we would like to produce a small model as a proof of concept which can be demonstrated at the end of the REU.

1. T. Chen, “Using Machine Learning Techniques to Analyze Sea Ice Features Using ICESAT-2 Data”.
2. “Finding Similar Items”. From a currently unknown textbook.
3. S. Puri, “Jaccard Similarity and LSH Applications,” ACM, Jun. 2022, doi: https://doi.org/10.1145/nnnnnnn.nnnnnnn.
4. C. Fu and D. Cai, “EFANNA : An Extremely Fast Approximate Nearest Neighbor Search Algorithm Based on kNN Graph.” arXiv, Dec. 03, 2016. Accessed: Jun. 01, 2022. [Online]. Available: http://arxiv.org/abs/1609.07228
5. C. Fu, C. Xiang, C. Wang, and D. Cai, “Fast approximate nearest neighbor search with the navigating spreading-out graph,” Proc. VLDB Endow., vol. 12, no. 5, pp. 461–474, Jan. 2019, doi: 10.14778/3303753.3303754.
6. C. Cai and D. Lin, “Find Another Me Across the World – Large-scale Semantic Trajectory Analysis Using Spark.” arXiv, Apr. 02, 2022. Accessed: Jun. 01, 2022. [Online]. Available: http://arxiv.org/abs/2204.00878
7. Y. Kalantidis and Y. Avrithis, “Locally Optimized Product Quantization for Approximate Nearest Neighbor Search,” in 2014 IEEE Conference on Computer Vision and Pattern Recognition, Jun. 2014, pp. 2329–2336. doi: 10.1109/CVPR.2014.298.
8. T. Ge, K. He, Q. Ke, and J. Sun, “Optimized Product Quantization for Approximate Nearest Neighbor Search,” in 2013 IEEE Conference on Computer Vision and Pattern Recognition, Jun. 2013, pp. 2946–2953. doi: 10.1109/CVPR.2013.379.
9. Y. Matsui, Y. Uchida, H. Jegou, and S. Satoh, “A Survey of Product Quantization,” vol. 6, no. 1, p. 9, 2018.
10. H. Jégou, M. Douze, and C. Schmid, “Product Quantization for Nearest Neighbor Search,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 33, no. 1, pp. 117–128, Jan. 2011, doi: 10.1109/TPAMI.2010.57.

This project has the opportunity for me to learn GPU programming which is something that I’d be interested in however Dr. Puri thinks that it is not needed and most of the GPU accelerated libraries use CUDA which I cannot use since my laptop does not have an NVIDIA GPU. I could investigate HIP which is the AMD competitor to CUDA but does not have the same level of support that CUDA does. I am presently unsure if the programming portion of this project will be conducted in python or C++. These are the libraries that Dr. Puri sent me:

• Clipper (C++) A computational geometry library specializing in shape intersections.
• Shapely (Python) A computational geometry library.
• E2LSH (C++) A locality sensitive hashing library which can compute exact nearest neighbors for polygons. This would be useful as a base line to compare any approximate approaches against.

I have also identified these libraries:

• FALCONN (C++) A more recent update to E2LSH apparently.
• Scipy Spatial (Python) Part of the greater scipy package and does have limited nearest neighbor capabilities using KD-trees.

As for other pros and cons, I am more familiar with python at a whole then C++, but I am proficient in C++. Additionally, using C++ would be faster and I am be any to leverage an intermediate stage of parallelism: CPU multi-threading. This is possible in python but certainly not something that python is good at and would probably be easier then having to learn GPU programming from the ground up since have conceptually background on CPU threading. Unfortunately MTU uses a library called ThreadMentor which is not available outside of MTU department servers in any practical manner so I would have to learn the C++ standard library interface. It does look like semaphores would require C++ 20, which may or may not be supported on the department server here at Marquette that I should be getting access to in the coming days.

I an tentatively calling this project “Approximate Nearest Neighbor Searches of Real World Geometry”, but this title is subject to change once the problem becomes well defined.

Thursday, 02 June 2022

Today I continued the literature review regarding approximate nearest neighbor searches. I read three articles which I had identified yesterday:

1. C. Fu and D. Cai, “EFANNA : An Extremely Fast Approximate Nearest Neighbor Search Algorithm Based on kNN Graph.” arXiv, Dec. 03, 2016. Accessed: Jun. 01, 2022. [Online]. Available: http://arxiv.org/abs/1609.07228

   While the graph based approaches to this do provide excellent results, the memory constraints are higher than the LSH methods used in the comparison. While the datasets used here are not as large as the ones mentioned in Dr. Puri’s LSH Applications paper, if we assume a linear memory growth, I’m not convinced that an approach like EFANNA is off the table.

2. C. Cai and D. Lin, “Find Another Me Across the World – Large-scale Semantic Trajectory Analysis Using Spark.” arXiv, Apr. 02, 2022. Accessed: Jun. 01, 2022. [Online]. Available: http://arxiv.org/abs/2204.00878

   This paper uses minhashing, a type of LSH to find similar semantic trajectories, basically people with similar life styles based off of the places that they visit, the order of places and the amount of time spent there. They developed a hashing method called Sequence-Sensitive Hashing (SSH) which was designed to respect the sequential nature of this data. It was interesting to see LSH outside of the textbook chapter that I read about it, but the data here is still rather similar to the document structure that LSH is frequently practiced on.

3. T. Ge, K. He, Q. Ke, and J. Sun, “Optimized Product Quantization for Approximate Nearest Neighbor Search,” in 2013 IEEE Conference on Computer Vision and Pattern Recognition, Jun. 2013, pp. 2946–2953. doi: 10.1109/CVPR.2013.379.

   This paper was somewhat of a break from the other two. Product Quantization is an approach which is adjacent to LSH and serves, at least to my current understanding, as a “different backend” for this whole process. It involves breaking the data space into a number of subspaces such that the original space is the Cartesian product of the subspaces. This produces distortion in the quantization process, which must be minimized to push for better results. The authors were able to find a non-parametric solution to this issues which can optimize the distortion in an iterative manner and it performed very well. Additional specialization is discussed for data which follows a Gaussian or normal distribution.

I additionally identified six libraries which may be relevant to this project once programming begins.

1. annoy (C++ / Python) Since when did Spotify develop things like this? Thanks to the NetworkX Core Development Team for this recommendation.
2. EFANNA (C++) EFANNA implementation.
3. NSG (C++) NSG implementation by the EFANNA authors. This is their improvements on EFANNA I believe, but while I have the research paper for NSG I have not had the chance to read it.
4. kGraph (C++ with limited Python support). ANN graph approach using a technique called NN-descent. Used as a benchmark for EFANNA.
5. FLANN (C++ / Python) KD-tree based algorithms.
6. yael (C++ / Python) Not sure what algorithms this uses but it was linked off the website for the datasets used in multiple of the papers I read today.

The datasets of this website where used in the Fu and Cai paper and Ge et al. papers, which may or may not be interesting resources to look at. I believe that these data sets are just numeric vectors in 128 or 960 dimensions which is idea for research on approximate nearest neighbor search (ANNS).

Looking at the programming resources that I have found, C++ is starting to pull ahead of my innate desire to program everything in python. I do not believe that this decision needs to be made this week.

One of the most important things for me to do this week is to find a narrow and tailored research topic. It looks like there as been a lot of research, which I am currently crawling through, on the general ANNS problem. However, I have not seen anything about using these techniques on shapes or other geometries. The Cai and Lin paper is probably the closest when it was discussing coordinate based similarity in their trajectories. I do need to investigate this specific sub-problem further, but I suspect that finding a suitable hashing or quantization function for the input geometries will be the heart of this problem. Once the LSH hashes or PQ codebooks are produces, I don’t see why existing methods like EFANNA or the algorithm described by Ge et al wouldn’t be applicable. However, if my experience with Google’s Summer of Code last year taught me anything it is that my last statement is almost certainly wrong and I just don’t have the knowledge yet see the problem and find a solution.

Friday, 03 June 2022

Today was another day of literature review. I read several papers, given by the below citations. I have written a few sentences about each article.

1. Y. Cao, T. Jiang, and T. Girke, “Accelerated similarity searching and clustering of large compound sets by geometric embedding and locality sensitive hashing,” Bioinformatics, vol. 26, no. 7, pp. 953–959, Apr. 2010, doi: 10.1093/bioinformatics/btq067.

   This was a very interesting paper, and even though it was about chemical compounds, most of their work was about euclidean space which makes in intimately practical for my work with geometry which is by euclidean by definition. The interesting thing is that this work focused on a high number of dimensions, generally over 100 to create the embedding in the EI-Search and EI-Cluster algorithm. Their process picks a subset, generally three times the number of dimensions of the data to create a reference embedding then minimizes a “stress” function, basically minimizing the mean squared error of the difference between the new addition and the old reference points. Their implementation of the EI-Search algorithm can be found here and they reference using L-BFGS-B library (which scipy does have this algorithm minimized) and lshkit library which make or may not become useful.

2. B. Matei et al., “Rapid object indexing using locality sensitive hashing and joint 3D-signature space estimation,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 28, no. 7, pp. 1111–1126, Jul. 2006, doi: 10.1109/TPAMI.2006.148.

   This paper was difficult for me to fully understand since it uses a lot of math notation that I was not familiar with, including ξ, Ξ and ζ which are not used frequently in the areas of math I am used to. It contacted several references which I did find useful, but I’m not sure how much I learned from it otherwise.

3. M. Astefanoaei, P. Cesaretti, P. Katsikouli, M. Goswami, and R. Sarkar, “Multi-resolution sketches and locality sensitive hashing for fast trajectory processing,” in Proceedings of the 26th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Seattle Washington, Nov. 2018, pp. 279–288. doi: 10.1145/3274895.3274943.

   This paper was the real winner of the day. It was on the other side of Find Another Me Across the World – Large-scale Semantic Trajectory Analysis Using Spark, doing coordinate based trajectory similarities. Their algorithm places random disks on the area of interest and by tracking if the trajectories entered the circle. This hamming distance of these binary sketch of the trajectories can be used as an LSH encoding for Hausdorff distance, which is the maximum minimum distance needed to travel between two curves. By recording the order of the intersections of the circles, they produce an LSH hash family for the Frechet distance which is basically the minimum “leash” distance needed to link two points on different curves when you can only move forward on the curve. This is the more useful metric for curves. The use of randomly placed circles does remind me of the fingerprint example from the textbook chapter that I was sent. I think that trying to change this method of randomly placed circles to use the Jaccard distance, which is just 1 - Jaccard similarity, we may be able to approximate the nearest neighbor. With a fixed number and size of each circle, the preprocessing for each shape would be linear in terms of the number of circles which would be much less then the number of shapes required for the brute force all pairs solution and their data structure, the Multi-Resolution Trajectory Sketch, could be an efficient basis for a query structure. I suspect that the complexity of the Jaccard distance with the circles would be more intense then if a trajectory intersected a circle, and if so performance would never match.

4. G. Mori, S. Belongie, and J. Malik, “Shape contexts enable efficient retrieval of similar shapes,” in Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. CVPR 2001, Kauai, HI, USA, 2001, vol. 1, p. I-723-I–730. doi: 10.1109/CVPR.2001.990547.

   This article was an interesting read with a surprising connection to graph theory matchings that I enjoyed. However, all of their preprocessing and query operated involved at least one level of iteration over the whole dataset. For the case of the shapemes which were faster to query, the preprocessing is O(Nk) where N is the number of shape contexts (which are also expensive to compute) and k is the number of shape pieces used in the algorithm which is also an expensive operation before we get to the O(Nk) peice. This method is certainly too slow to be of use to us for this project.

   It was, however, the third paper which I saw that referenced Indyk and Motwani so that will have to be the next paper that I read. A full citation is given below.

P. Indyk and R. Motwani, “Approximate nearest neighbors: towards removing the curse of dimensionality,” in Proceedings of the thirtieth annual ACM symposium on Theory of computing  - STOC ’98, Dallas, Texas, United States, 1998, pp. 604–613. doi: 10.1145/276698.276876.

I also found this paper, with a new author but with the same name and 14 years more recent. I will have to find the difference and connections between these papers.

S. Har-Peled, P. Indyk, and R. Motwani, “Approximate nearest neighbors: towards removing the curse of dimensionality,” Theory of Comput., vol. 8, no. 1, pp. 321–350, 2012, doi: 10.4086/toc.2012.v008a014.

Week 2

Monday, 06 June 2022

Attended responsible conduct in research training.

Tuesday, 07 June 2022

The end is hopefully approaching for my literature review. Today I read

1. P. Indyk and R. Motwani, “Approximate nearest neighbors: towards removing the curse of dimensionality,” in Proceedings of the thirtieth annual ACM symposium on Theory of computing  - STOC ’98, Dallas, Texas, United States, 1998, pp. 604–613. doi: 10.1145/276698.276876.

   This is one of the most referenced papers that I’ve seen during the rest of my literature review, and I probably should have read it sooner. However, it seems that this paper was a big break through for approximate nearest neighbor (ANN) searches of high dimensional vectors, like other papers dedicated solely to ANN improvements have been working with. The authors use a new type of data structure called a ring-cover tree which can reduce the complexity of the ANN searches to only mildly exponential. According to the paper “For 0 < ε < 1 there is an algorithm for ε-NNS in R^d under any l_p norm which uses O(n) x O(1/ε)^d preprocessing and requires O(d) query time” [1]. This is great in and of itself, but it doesn’t translate well to my project which involves shapes and geometries. Basically, if I can reduce each shape to a vector in R^d for some constant d (which I think that I can do), then I could use methods. However, if that is the case, there are C++ libraries using more efficient algorithms like EFANNA or NSG which I could leverage without needed to implement a ring-cover tree.

2. S. Har-Peled, P. Indyk, and R. Motwani, “Approximate nearest neighbors: towards removing the curse of dimensionality,” Theory of Comput., vol. 8, no. 1, pp. 321–350, 2012, doi: 10.4086/toc.2012.v008a014.

   Basically, [1] is a conference paper and this is the journal paper. We recently talked about the difference between the two types of papers in one of the REU lectures. A conference paper is presented at a conference and normally shorter or more preliminary results. Then, later the authors will revise the paper and contribute at least 30% more new content and them publish a journal paper which is just an expended version. All of the arguments about [1] also apply here, but the content was presented in a more concise format with some new generalizations and applications such as an approximate minimum spanning tree algorithm and extension to normed spaces rather then hamming distance discussed in the conference paper.

3. J. Ji, J. Li, S. Yan, Q. Tian, and B. Zhang, “Min-Max Hash for Jaccard Similarity,” in 2013 IEEE 13th International Conference on Data Mining, Dec. 2013, pp. 301–309. doi: 10.1109/ICDM.2013.119.

   This paper was actually very interesting. It is a refinement on min hashing (sometimes referred to as min-wise hashing). The in the traditional min-hashing approach is to permute the two sets K times and only look at the hash value of the first element of the permutation. It can be mathematically proven that the probability of this value being the same for two sets converges to the jaccard similarity of the sets. This paper introduces a refinement to this idea called min-max hashing where instead of needing K permutations to generate a length K sketch, you only need to generate K/2 permutations and take the first and last values from the resulting re-ordered sets. Since generating and evaluating the permutations (which for practicality reasons we never fully apply to the dataset) is the most time consuming part of the min-hash algorithm, min-max hashing halves the computation time and actually improves the MSE of the approximate jaccard similarity by in effect sampling without as much replacement from the possible first elements of the permutations. In practice it seems that the variance improvements are detectable but not significant. However, the computation benefits more then justify using this technique if I end up using a min-hashing approach.

4. O. Chum, M. Perd’och, and J. Matas, “Geometric min-Hashing: Finding a (thick) needle in a haystack,” in 2009 IEEE Conference on Computer Vision and Pattern Recognition, Jun. 2009, pp. 17–24. doi: 10.1109/CVPR.2009.5206531.

   I do not think that this paper will be relevant to my project, however some of the notions may be applicable and you never know what will become important. This paper is using images and the idea of visual words which I believe are simple geometric patterns that can be identified with a feature extractor like a specific curve or likewise. Note that a feature from the feature detector can contain multiple visual words. The author’s use primary visual words and features who are composed of only one visual word and a set of secondary visual words, visual words which are selected in the general proximity of the primary visual word with some restrictions on the distance and sizes allowed. Once the signatures are generated in this manner the rest of the process is very similar to the traditional min-hashing approach, but the more careful generation of the signatures proved very helpful in improving the results of the traditional min-hashing algorithm.

I have identified one more C++ library. This one is CGAL and it does have the capabilities of reading the input format that the datasets that I have identified will be presented in (more on that below). More exploration is needed to see the full extent of it’s support.

Also, I met with Dr. Puri today and learning several things. First, the textbook chapter that he sent me has the full citation presented below:

• J. Leskovec, A. Rajaraman, and J. D. Ullman, Mining of Massive Datasets, 2nd ed. [Online]. Available: http://infolab.stanford.edu/~ullman/mmds/book.pdf

There is also a third edition of this book, which is listed as having new information about min-hashing:

• J. Leskovec, A. Rajaraman, and J. D. Ullman, Mining of Massive Datasets, 3rd ed. [Online]. Available: http://infolab.stanford.edu/~ullman/mmds/book0n.pdf

During that same meeting with Dr. Puri we also discussed several technical components for the project. First, I can get datasets from UCR Star, a repository of real-world spatial datasets represented in the well-known text format. We decided that for the time being we do not need to consider the rotation of the shapes, i.e. if I rotate a square 45 degrees it is now considered a different shape when it was before. This should save a lot of time during the preprocessing steps, but accuracy of the model would certainly be improved if we could detect and rotate the shapes as needed. The only method for overcoming this that comes to mind immediately is to find the longest angle bisector in the polygon (quick StackOverflow link in case I have time for this.) and try to align it to be either vertical or horizontal in hopes that it would cause very similar shapes to be detected.

Additionally, Dr. Puri doesn’t seem concerned about needed to translate the shapes to be centered on the origin, but I am. Intuitively the jaccard similarity is the intersecting area over the union of the two shapes. If the shapes are not touching or overlapping at all then the similarity will always be zero (and thus the distance variant always one) even if it is the same shape that has been translated in a random direction. It is possible that the computational geometry libraries that I will leverage are able to account for that, but I’m not sure if they will. If not, it will be necessary to translate the shape so that the centroid, sometimes called a barycenter, is at the origin. According to the wiki page linked previously, if can find the centroid of a polygon with an O(n) operation where n is the number of vertices in the polygon. I have actually already had to implement this for Altas, a class project at Michigan Tech and I remember that something with signed area of zero was very problematic, so I hope that I don’t have that issue this summer. (link here) I think that is it unlikely since we were using a lot of artificially generated geometry in that project and not real world data like in this case.

It turns out that this problem was inspired by a problem that the National Geospatial-Intelligence Agency published as a project. This project was actually to use images from social media which have been stripped of metadata to find the nearest neighbor (or approximate nearest neighbor) in a database with tens of terabytes of geo-tagged images to help identify where the image was taken, which would be useful in both helping first responders in disaster sites or locate other individuals of interest to the government. While that first one is absolutely beneficial, the second use certainly has some ethic consideration. This project may be inspired by that work, but we are not using images of any kind in this project. Information in the NGA grant can be found below.

• “BIG-R BAA Topic 4: High Dimensional Nearest Neighbor.” Mar. 15, 2021. [Online]. Available: https://www.grants.gov/web/grants/search-grants.html?keywords=HM0476-20-BAA-0001

Dr. Puri also recommended looking into spatial hashing and z-order curves which are methods for taking discrete x and y coordinates and transforming them into one value that can be used in a traditional one dimensional hash table. I’m not sure if or when I will need to use these at the moment, but I did find two papers on spatial hashing which I will probably read tomorrow.

• S. Lefebvre and H. Hoppe, “Perfect spatial hashing,” ACM Trans. Graph., vol. 25, no. 3, pp. 579–588, Jul. 2006, doi: 10.1145/1141911.1141926.
• E. J. Hastings, J. Mesit, and R. K. Guha, “Optimization of Large-Scale, Real-Time Simulations by Spatial Hashing,” Proc. 2005 Summer Computer Simulation Conference, vol. 37, p. 9, Jul. 2005, [Online]. Available: https://www.eecs.ucf.edu/~jmesit/publications/scsc%202005.pdf

I also got login credentials to everest, a sever run by Marquette University to conduct my research on. I am planning on making a concurrent program to help move through the datasets I will be working on (generally gigabytes in size with millions of records). I would like to use the C++ standard library for my threading. That was introduced in C++11, and counting_semaphore was not introduced until C++20 so I had to determine which C++ standards were available on everest. Using the below script, I found that complying without the -std flag defaults to C++98 and that up to C++11 is supported. Since counting_semaphore is not among these, if I need can either use monitors or use a monitor to create my use semaphore. From my experience in concurrent, I will probably choose the latter. On the off chance that the C++ threads are limited to only one core (which I think is very unlikely) I will have to move to POSIX threading using pthreads.

   #include <iostream>
   
   using namespace std;
   
   int main()
   {
       if (__cplusplus == 202002L) cout << "C++20" << endl;
       else if (__cplusplus == 201703L) cout << "C++17" << endl;
       else if (__cplusplus == 201402L) cout << "C++14" << endl;
       else if (__cplusplus == 201103L) cout << "C++11" << endl;
       else if (__cplusplus == 199711L) cout << "C++98" << endl;
       else cout << "pre-standard C++" << endl;
   
       return 0;
   }

Wednesday, 08 June 2022

More research papers! Today I read the below papers:

1. B. R. Vatti, “A generic solution to polygon clipping,” Commun. ACM, vol. 35, no. 7, pp. 56–63, Jul. 1992, doi: 10.1145/129902.129906.

   This is the original research paper for the general polygon clipping algorithm used as part of the clipper library which I will need to compute the jaccard distance for the shapes in my datasets. Technically, since I am planning on using a library for this, I did not need to read the paper. However, a lot of time in ANN search research is spent on the complexities of the data structure and processes so a generally understanding of the algorithm it to my direct benefit. The algorithm itself sweeps the overlapping polygons from bottom to top and divides edges into two categories; contributing or non-contributing. Contributing edges effect the final result of the clipped polygons while non-contributing ones do not. The paper lies up several rules which can be used to determine which is which. According to the paper, the total complexity of the algorithm is linear with respect to the total number of edges between the target and clipping polygon.

2. C. Fu, C. Xiang, C. Wang, and D. Cai, “Fast approximate nearest neighbor search with the navigating spreading-out graph,” Proc. VLDB Endow., vol. 12, no. 5, pp. 461–474, Jan. 2019, doi: 10.14778/3303753.3303754.

   This was another paper about ANN, or more accurately AKNN. It builds on the EFANNA paper to further improve on four aspects which the authors have deemed important for a graph based ANN approach:

   1. Guarantee that the graph is connected, so that the query is always reachable.
   2. Reduce the average out-degree of the graph which improves search time.
   3. Shorten the path from the starting node to the query, which also improves search time.
   4. Reduce the memory usage of the graph to improve scalability.

   To accomplish these goals, the authors adapted the idea of a relative neighborhood graph which is a graph on a set of points for which the longest side of each possible triangle on the set of points. However this is actually a too selective process and can lead to non-monotonic paths in the graph, i.e. paths were the only way to get closer to the query point is to temporarily move away from it. They then develop the idea of a monotonic relative neighborhood graph (MRNG) where certain edges that wouldn’t be included in the RNG are added back. The naive implementation of this O(n^2 log n + n^2 c) where c is the the average out-degree of the graph, which is clearly unacceptable for large datasets. However, it is possible to approximate the MRNG with the navigating spreading-out graph (NSG) which starts with the nearest neighbor graph (or an approximation of it, like from EFANNA) which only ensures a monotonic path from one starting location, chosen to be the mediod of the data, to all other points in the dataset. This approach leads to the fastest index building times and the smallest index which makes NSG the known graph based method. While it’s memory usage is still higher then some LSH methods, the authors were able to test it on a 100 million point data set on a machine with 96 Gb of ram successfully, so it should work for my datasets if applicable. That last bit is the trick here… Is a possible to adapt this for what I need? The original algorithm is defined only for the L2 norm do if I can use that distance measure at some point, I should be ok. If a need to use something like Manhattan distance or something more exotic I may have more problems.

Thursday, 09 June 2022

I finally did it! A day of research which did not involve be reading research papers for 6 to 8 hours!

So, if I wasn’t reading all day, what did I do?

1. Create the daily log from yesterday (I know, I just forgot before going to bed last night).
2. Fleshed out the stub page for my REU project, attempting to find research goals and summarize the problem. Recall that the project is called Approximate Nearest Neighbor Searches of Real World Geometry.
3. Started trying to formulate the plans and theoretical properties that I am going to need to prove the correctness of whatever system I develop and explore different methods that I could follow. That document is typeset in LaTeX given the higher mathematics dense then I could reasonably support in this wiki (please give us MathJax or KaTeX on the wiki) and I have emailed it to Dr. Puri to get his feedback on it.
4. It seems like everest does not have all of the dependencies for some of the libraries that other researchers have developed so I also inquired into what process will be needed to install those. If they cannot be installed there are work-arounds but they will be slower and I will not have time nor the ability to rewrite these libraries at the same level of optimization.

Friday, 10 June 2022

1. Y. Liu, J. Yang, and S. Puri, “Hierarchical Filter and Refinement System Over Large Polygonal Datasets on CPU-GPU,” in 2019 IEEE 26th International Conference on High Performance Computing, Data, and Analytics (HiPC), Dec. 2019, pp. 141–151. doi: 10.1109/HiPC.2019.00027.

This was another paper sent to me by Dr. Puri and it is about using a hierarchical filtering system to perform operations like spatial join over large geospaital datasets. To do this they developed the notion of a PolySketch which is based off breaking the polygon or line into segments then find the minimum bounding rectangles. Finding the intersections of the rectangles is easier then of the polygons themselves due to the simpler geometry. The usage of minimum bounding rectangles is more traditional within the land of computer graphics and very easy to work with. This is however different from “Multi-resolution sketches and locality sensitive hashing for fast trajectory processing” by Astefanoaei et al which has been one of my important references since they use circles. The circles are an important choice since offsetting them in any direction will produce the same area profile which they use build the probabilistic bounds needed for proving the LSH family’s properties. Because of this, the use of circles here is going to be similarly important to this work. Unfortunately I do not believe that Clipper has dedicated circle support which means that I will have to use an approximation but of course the computational complexity of computing the Jaccard distance varies linearly with the total number of vertices between both so the better the approximation the longer the operations will be. This will likely become a user setting.

In addition, I began to consider some of the more technical details of the project. I am currently thinking that I will start testing with the lakes dataset on UCR Star. This set is 7.4 GB and has 8 million records and can be downloaded in

• GeoJSON
• CSV
• KMZ
• Shapefile
• JSON+WKT

This means that I have a choice about how I want to parse this data. Python has much better support for these data formats than C++ does (shocker, I know), so there will likely be a preprocessing step done in python. Please note that for all of these ANN searches, the time to build the index is critical to evaluating the method, so I cannot do too much with this. I have downloaded a sample of the lakes dataset in both JSON+WKT and CSV and both of them contain the WKT data, just embedded in different data storage formats for the auxiliary data like the name of the body of water. I am currently not sure if this auxiliary data will need to be preserved in the final data structure, but it may be useful. Python does have a JSON library and CSV is not overly difficult to parse through, but I plan to use Clipper for Jaccard distance which does not read WKT so I will most likely parse each WKT representation to a text file where each point is a new line, which would be very easy to read in C++.

Another possible preprocessing data step might be to center each of the polygons around it’s centroid so that the step doesn’t need to be repeated while working on only the data structures. However, this is an important part of the creation of the data structure indices, so the option to perform it in the C++ portion of the code should at least exist.

The data is very large and I would like to preprocess concurrently so first I’d split the file into manageable chunks. On linux systems, sed -n '$=' <filename> can find the number of lines in a file and split -l <number> <filename> will split the file into chucks with the given number of lines. By combining these I can create the correct number of new files programmatically based on the number of processes that will be run.

Week 3

Monday, 13 June 2022

Today I worked on setting up my development environment on everest. I think that using some of the libraries that I have discovered I can develop this application excursively in C++ using tools like

• GEOS - the computational geometry library that shapely wraps. Note that the C++ API is unstable, but I don’t expect to be updating the library during the course of this summer. Additionally, it is possible to run C code in C++ and the C API for GEOS is stable. GEOS has WTK and GeoJSON readers. Another advantage for the C interface is that their are reentrant versions of most of the functions.
• gnuplot - command line plotting library that I found a C++ wrapper for. I actually used gnuplot in high school for a few weeks plotting paths for the robotics team I was a part of.

And I started by installing gnuplot locally on everest, which was not that difficult to build from source. The tricky part was the C++ integration with gnuplot. This is a single C++ header file which uses POSIX pipes to connect to the gnuplot binary which I put unto my PATH. Since I am running only an ssh connection to everest, it does not connect to the X server and naturally the DISPLAY environment variable is left undefined. This is fine since I can set gnuplot to output a png, jpeg or a whole host of other file types instead of displaying an X window. The C++ header file that I found even includes a static method called set_terminal_std to set this value. However, I was constantly getting an exception saying that the DISPLAY environment variable could not be found. After trying every imaginable combination of where and what to call set_terminal_std with I finally opened the header file to track down the problem, which I had determined was coming from the constructor for the gnuplot object using valgrind. At the top the init function used by all of the various constructors I found this (starting at line 1694):

   #if ( defined(unix) || defined(__unix) || defined(__unix__) ) && !defined(__APPLE__)
       if (getenv("DISPLAY") == NULL)
       {
           valid = false;
           throw GnuplotException("Can't find DISPLAY variable");
       }
   #endif

So, even if I was already using the static method set_terminal_std to change the terminal type to output a png, it was always still going to error. Looking at the source code for set_terminal_std (which was included in the doxygen documentation that I had generated) I was able to correct this line to the below code so that if the terminal type was x11, the default value and the DISPLAY variable couldn’t be found it would generate the exception.

   #if ( defined(unix) || defined(__unix) || defined(__unix__) ) && !defined(__APPLE__)
       if (terminal_std.find("x11") != std::string::npos && getenv("DISPLAY") == NULL)
       {
           valid = false;
           throw GnuplotException("Can't find DISPLAY variable");
       }
   #endif

And suddenly everything was working properly.

Getting GEOS to work was also very difficult. In order to even install it I had to download a more recent version of cmake and configure my PATH to find that before the version already on everest. But in the scheme of things, that was easy compared to what came next. I decided to write a small program using GEOS which read the large polygons that Dr. Puri had sent. The GEOS documentation was not very helpful. While they did warn that the C++ API was unstable, I thought that it would be fine since I would only need to work with the current version. However, there were type alaises and functions which

1. The most recently documentation includes
2. StackOverflow posts from almost 10 years ago include
3. The header files themselves include, but yes I got to the point where I was reading them

But g++ couldn’t find them. Eventually, after about 5 hours I was able to read the shapes and find the function call to perform an intersection of the shapes (since that is what this library will be doing for me, in additional to reading the geometry from the data files) to be meant with an error message about “non-noded intersections” which I definitely did not understand. Google searches showed that many other programmers using computational geometry libraries were encountering this, but the term “non-noded geometries” was not formally defined anywhere and explanations about what exactly it is varied but included self-intersecting polygon and line segments which were sitting too close to each other.

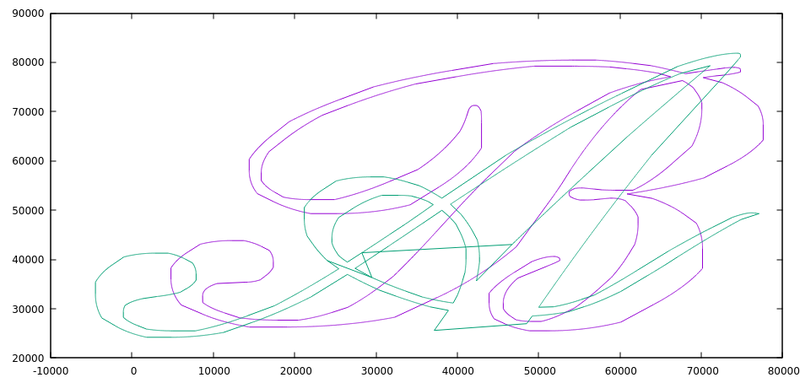
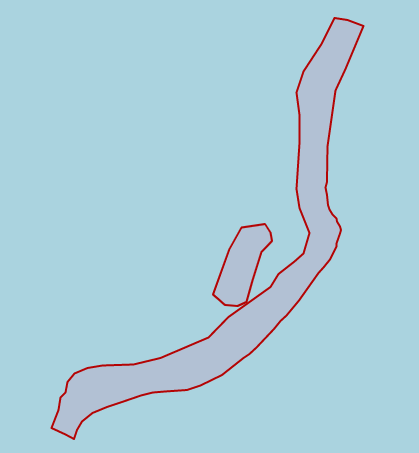
So I decided that I needed to see the shapes to understand if anything was wrong. Them in gnuplot revealed what I believe is the problem.

And finally the two overlapping, which is specifically what I’m interested in.

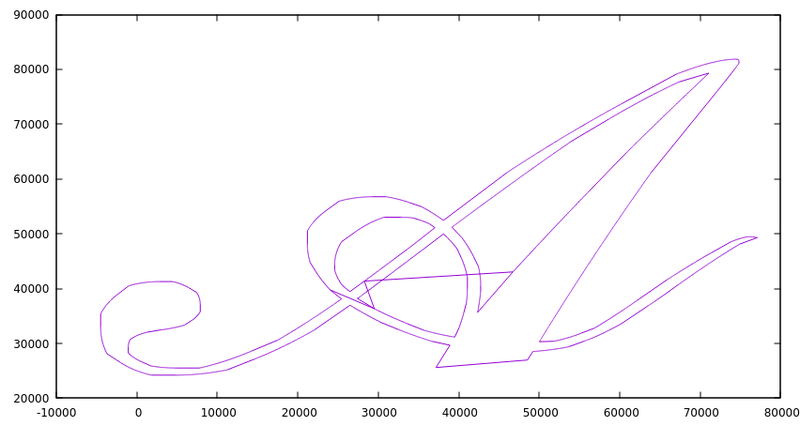
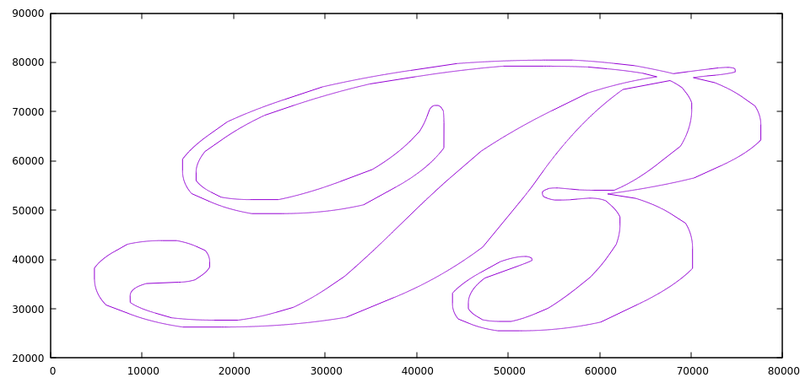
I really thing that the problem is coming from the weird zig-zag on the A and tomorrow I will try to remove that from the data file to see if my results improve. Additionally, I should try to rewrite this same program using Clipper, which is the library that Dr. Puri recommended. The API seems much simpler but it doesn’t have the ability to parse from know formats like WKT or GeoJSON. I will probably also try to rewrite the same program in GEOS but using the C API (which as mentioned before can be mixed) since the C API has reentrant versions of most of the functions which will be important when using a multi-threaded application. Otherwise, I may have to add synchronization primitives like mutexes around GEOS calls which would reduce much of the concurrency. I only hope that the C API is easier to understand and has more accurate documentation then the C++ one, but that is a tomorrow problem.

Tuesday, 14 June 2022

The battle with GEOS entered its second day today, but progress was definitely made. As I suspected, the library did not like the self-intersecting geometry of the script A shape. I was able to manually identify where each of the holes in the shape started and break up them up into separate text files with the help of a small python script that I wrote which calculated the length of each edge and reported them sorted from longest to shortest, since it seemed reasonable that the erroneous edges would be among the longest.

Once I developed the code to create the A using the proper geometry, I was finally able to get the intersection operation to work. In case you were curious, the intersecting areas of the two shapes as below.

Error creating thumbnail: Unable to save thumbnail to destination

However, the inconsistencies with the posted documentation for GEOS and the code that ended up where bothering me. I understand that the C++ API is unstable, but the amount of change between 3.10.3, the latest release and the current 3.11 beta that the online documentation was feeling off. Additionally, code from StackOverflow from well before that version was released also had the features that my program was unable to find.

I suspected that the program was being complied with a different version of GEOS other then 3.10.3 which is what I wanted to be running. First, I was able to confirm that several older versions of GEOS were on the system, but I still not sure which version g++ was finding during the linking process. I eventually tracked down a function called geosversion() which just returns the version number as a string. The return result was 3.5.1 which was released in 2016 and explains some of the issues I was having with the API.

So I started trying to link directly to 3.10.3, and that was certainly a process. I tried setting -I and -B flags on g++ but to no successful. Either it was linking against the wrong set of headers and I was getting errors about various types or functions being undefined or everything was complaint with the headers and during the linking process I was getting a wall of undefined reference errors. I was helped by a set of credentials that Dr. Puri provided for an account that had already set up a newer version of GEOS locally. This helped me realize that instead of -B I such be using -L in combination with the -lgeos flag.

This really reduced the number of undefined reference error that I was seeing, but did not eliminate them entirely. Since it was obviously finding part of API (but not all of it) I decided to check out the GitHub for GEOS to see where and how those functions and constructors were defined. I found that they were defined in some .inl files which were only included if a preprocessor macro called GEOS_INLINE was defined. Some research shows that .inl are used to de-clutter headers which might otherwise have one line or inline function definitions. I don’t know why GEOS is setup like this or how to define GEOS_INLINE otherwise (which is something that really should be in the documentation). Once I defined this macro and used the below command I was able to successful compile and run the program which did the same thing as before, read the A and B, find the intersection and write the output.

   g++ -std=c++11 -o ngc new_GEOS_clipping.cpp -D GEOS_INLINE -I ~/usr/local/include -L ~/usr/local/lib64/ -lgeos

I hope that the perks of having the WKT and GeoJSON parsers will make the effort worth it, but so far I am not impressed with GEOS. I do still need to try to use the C interface which is reentrant but also not object oriented (which may be a good thing, I don’t know yet).

Wednesday, 15 June 2022

Today I reworked the program I’ve been writing for the last two days to use the GEOS C API rather then the C++ interface. After everything that I’ve learned from the painful experience of using the C++ API seems allowed me to pick up the C API with minimal hassle.

Compile against the C API can be done with

   g++ -std=c++11 -o gcc GEOS_C_clipping.cpp -I ~/usr/local/include -L ~/usr/local/lib64/ -lgeos_c

While using #include "geos_c.h" in the source file. One helpful trick is to #define GEOS_USE_ONLY_R_API to use only the reentrant API in the program. Already this has caught multiple times were I was using the non-reentrant version of the API. Basically, so avoid the problems caused by non-reentrant functions the entire API has versions of the same functions which end in _r and take an extra parameter of type GEOSContextHandle_t which manages the per-thread context rather then using a global context which would potentially cause problems.

So far I have not had any problems using the C API from within a C++ program. In fact, there are warnings whenever I compile with the C++ interface that I should be using the C API. I suspect that the C++ interface is meant to be an internal one primarily which they have exposed to the public as a “just in case” measure. Of course the C API is a completely functional in nature and I will have to be a bit more careful about explicit memory management but I’m not that concerned since many of my classes at MTU required that level of attention to detail and we were frequently docked a few points if their were memory leaks in our programs.

Moving forward, I need to explore the geometry parsers such as for WKT and GeoJSON in GEOS so that will probably be what I do tomorrow. I will download a small sample from the lakes dataset, hopefully containing only a few dozen lakes and start working with parsing that into GEOS.

Thursday, 16 June 2022

This was once again a technical and programming day. I started the morning by refactoring the entire project structure in a way which I believe will facilitate the growth of the number of files and amount of data I will be processing this summer. In addition to doing things like separating the files based on categories like data, binaries, source and example code (which are the small programs I’ve been writing for the last two days to learn more about the GEOS APIs) I created a private GitHub repository so that the code can be properly backed up and version controlled. Additionally, I wrote a small script which will run clang-format on all of the .cpp and .h files that I write. Unfortunately, clang-format, which is built on the LLVM toolchain is not on everest and would be very complicated to install. This means that I am pulling the code from GitHub onto my laptop and running clang-format locally before pushing back up. This will introduce more commits, some of them just formatting changes, but I think that having well-formatted code is important.

After that, I downloaded a small subset of the lakes dataset from UCR Star, specifically this regions which is just to the west of Milwaukee. I downloaded it in several formats included CSV (which is actually TSV or tab separated values) where the first column is WKT, JSON+WKT were ever line started with a JSON key {"g":" before starting a WKT representation of shape and finally GeoJSON which is completely different but also supported by GEOS.

I then wrote functions which take one of those files and returns an array of GEOSGeomtry pointers after passing it through the readers for the relevant formats. I did not get a chance to write the GeoJSON one, but that is going to be a bit different since each object stretches over multiple lines of the file. I will unfortunately have to read the whole file into memory and then pass the whole thing to the GEOS GeoJSON reader. To keep the same return format I will then need to iterate over the internal geometries with something like GEOSGetGeometryN_r.

Additionally, the current methods for WKT and CSV are not truly reentrant since malloc is not reentrant and they both need to use that function. This is an advantage to the GeoJSON reader which shouldn’t need to use malloc at the cost of having to fit the whole file into memory instead of reading it line-by-line. For the whole lakes dataset I would likely have to increase the heap size to fit the whole dataset into memory. The WKT and CSV also have the advantage of one object per line, which means that I could theoretically break the file into set chucks (see command like split that I discussed above) which would take just as long the first time but open up the possibly of saving the chucks and being faster for later reconstructions of the database. Issues with malloc could be solved with a mutex as long as I don’t need to set things like signal handlers with malloc which would introduce the possibility of deadlock, but I don’t think that I will need to create any signal handlers or other functions which could interrupt the thread from within itself.

Tomorrow I will likely finish the GeoJSON reader, clean up some of the code, trying to make it reentrant, and create a util file which things like the GEOS message handler that I need to have (so that I don’t have to repetitively re-create it) and create a counting semaphore out of a monitor since that doesn’t exist in C++11. Finally I will create a brute force all-pairs Jaccard distance program which will find the most similar of the 264 bodies of water I have downloaded. Currently, I think that I should skip all geometries which are not polygons (like the rivers which are linestrings) since they are outside the scope of this project.

Friday, 17 June 2022

I am very concerned about having to build a semaphore using the C++11 standard library synchronization primitives. Race conditions can be subtle and I do not want to introduce a place for them to exist in a piece of code I wrote when it could be done using a library. Additionally, installing C++20 seems to difficult for the nature of this project, so when I design my concurrent solution it will use the C++ library if I decide to use monitors and pthreads if I want to use semaphores.

There was also an issue with the JSON+WKT reader that I wrote yesterday were the first line of the file was missing a space before the start of the JSON. This was more annoying and difficult to track down then it should have been.

After that I started to work on creating the helper function which can center a geometry around it’s centroid and find the Jaccard distance. I believe that I have a working implementation of the Jaccard distance, but it is very difficult to actually test without the centering code since Open Street Maps doesn’t define lakes which overlap other lakes so the results are always 1 which is correct. I have encountered some problems with the centering code however. Most of the accessors for the geometry return immutable data structures so I cannot manually translate the shape towards the origin. As far as I can see, there are two ways forward from this point.

1. Copy the data from the immutable structures into newly created mutable ones, perform the transformation and then create a new polygon to replace the older one. This is possible, but also very memory intensive since these are large, complex polygons that would have to be copied to secondary arrays multiple times and possibly in multiple chucks (if it has interior rings, like for an island).
2. Update from GEOS 3.10.3 to GEOS 3.11.0beta1 which has a function called GEOSGeom_transformXY_r which uses a user defined function to modify the points in the shape in-place with the help of private functions within the library.

Given that the second option is exactly what I need, on Monday I plan to attempt the update. If that fails, I will pursue option 1, but it will most likely be slower and definitely less memory efficient. Since I’ve already build this library from source multiple times when trying to configure it originally, I am not expecting any difficulties, but I suspect that I will be surprised about something.

Week 4

Monday, 20 June 2022

Today started out slow, but steadily picked up speed. I started by updating GEOS from 3.10.3 to 3.11.0beta2. Note that on Friday I said that I was going to update to beta 1, but earlier today they released beta 2 and took down the beta 1 tarball, so beta 2 was what I had to use. Like I suspected on Friday, the update was not as smooth as I expected, mostly due to an outdated line of my .bashrc. To facilitate linking with a local install of the GEOS library, I had set

export LD_LIBRARY_PATH=~/usr/local/lib:$LD_LIBRARY_PATH 

in the .bashrc, but then refactored the project to bring the shared library files into the project directory without updating it. It didn’t cause a problem at first since the versions were the same, but after the update it was linking against 3.10.3 and couldn’t find any of the 3.11.0 files until I tracked down and updated the .bashrc.

After that I was off to the races to fix the centering code using the new functions introduced to the C API in 3.11.0. Unfortunately these were not in-place operations like I thought they were but it was still easier then trying to create these functions myself or hacking my way around the immutable structures that GEOS likes to return to me. I spent several hours debugging the centering code, wrote a new method getCenter which wraps the process of using GEOSArea_r which still requires several more steps to extract the x and y coordinates as doubles rather then a GEOSGeometry pointer which points to a Point. This allowed me to verify that the centering was working and then… the Jaccard distance between the first two shapes in the data file didn’t change. This was of course possible (see below), but also unlikely. I soon realized that the first entry in the data that I downloaded was a LINESTRING and that my process for reading in the geometries wasn’t removing these. Fortunately, adding a check for this was fairly simple using an enum defined in geos_c.h. After that was fixed, it was time to finish the all-pairs search for the lowest Jaccard distance. With all of the components in place, a nested for loop was the only missing thing.

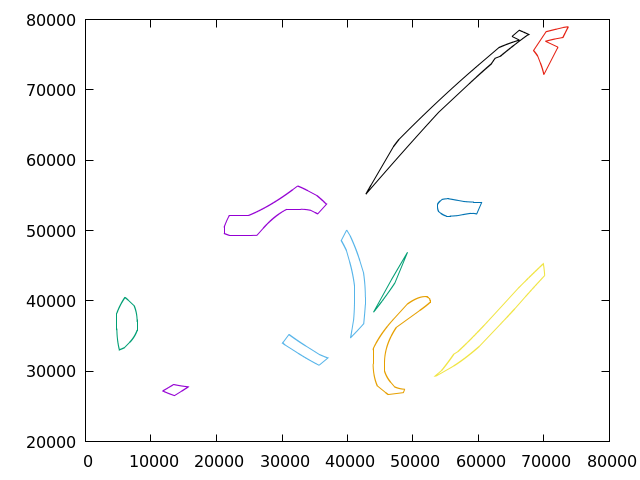
I also modified the code to search for both the minimum Jaccard distance and the maximum Jaccard distance. Both of these pairs are then written to WKT files. As much as I’d like to find a way to plot these locally, I have not found a good way to pipe these to gnuplot or found any other solution to generate plots from either point lists or WKT. There are web solutions, like the OpenStreetMap WKT Playground which I used to generate these screenshots of the most similar and least similar pairs of objects. All of the online WKT parsers plot the data on a global map. The solid blue background is because these are on a global scale, very small lakes which have been shifted to be centered at (0, 0) latitude and longitude which is near the Gulf of Guinea off the sub-Saharan south coast of Africa.

Error creating thumbnail: Unable to save thumbnail to destination

Error creating thumbnail: Unable to save thumbnail to destination

Moving forward, I think that I am getting close to being done with the pre-processing code itself. I do still need to investigate the precision capabilities of GEOS so that I am working at something more controlled than just raw double precision. Even if I scale all of the points to be integers, GEOS will always report doubles from its functions. However, not working with tiny decimals will reduce the chances of underflow and likely still be easier to work with. Additionally, I of course will eventually need to parallelize the reading process. For now that could be working with two threads on the existing small dataset that I have. Concerns would be ensuring everything is using the reentrant API for GEOS and the process of splitting the lines of the file between the threads. After that, I think that I need to send some more time working the the theoretical properties and structure of the LSH scheme before implementing it and design a concurrent solution to inserting and querying the resulting data structure.

Tuesday, 21 June 2022

I started investigating the precision handling capabilities of the GEOS C API. While it appears to be possible to simulate a global precision level in the C++ API by having the ability to pass a GeometryFactory to a WKT reader which would then inherit the PercisionModel of the factory, this capability has not yet been exposed in the C API, which in this respect is much more limited. While it is possible to change the precision on the output of a WKT writer, it don’t seem possible to set the precision on a WKT reader or even a global precision. It is possible set the precision on existing geometry, in effect snapping it to a grid of specified size, this would require another pass over the vertices of the geometry to cause the snapping effect. Another option does exist, however. I could incorporate this step into the centerGeometry function, specifically the transformer used to translate the polygons to be centered at the origin. I could scale them up by some factor of 10 (the data I downloaded uses 7 decimal places, so 10,000,000 may be a good choice) and then truncate anything left over, which would be nothing for 10^7 but using a smaller power of ten would lose some data.

While the above option would let me simulate the effects of the precision level on the polygons during the preprocessing phase, it would not be respected by any of the other GEOS operations. For example, taking the intersection of two polygons with a set precision will always yield a result within that same level of precision, such as for example 4 decimal places. However, if I use the scaling method purposed above, the precision set on the polygons during that same intersection operation will be the default value of floating. An easy option here would be to truncate or round the double back to an integer value, but that introduces potential inconsistencies if I forget to apply this methodology uniformly across the project. During my meeting with Dr. Puri we did discuss this. He left it up to may discretion, but did understand both the pros and cons to the approaches. I am personally leaning towards using a combination of the two; scale everything up to avoid underflow and then set the precision within GEOS so that all subsequent operations respect the desired precision.

Dr. Puri send my some code which uses GEOS to perform spatial joining operations written by one of his PhD students. Potentially useful parts of this code can be divided into two portions:

1. The spatial join itself: While LSH doesn’t assume that we can take the distance between multiple sets of objects at once, I do think that this aspect of the code could be helpful. I wouldn’t use it between members of the target dataset, but as part of creating the hash. If I follow the structure laid out in “Multi-resolution sketches and locality sensitive hashing for fast trajectory processing” I could use it to help find the intersections between each of the polygons in the dataset with the circles or squares or wherever shapes used to create the hash.
2. The code for parsing the data: This could definitely be useful and is exactly the type of thing were existing code has the potential to speed up a lot of my work. Upon reading the code, it does take a slightly different approach of reading the whole file into memory and using a multi-threading solution to parse the WKT into GEOS geometry objects where I was planning to split the file first using the split command and then pass the different files off to different threads which would read and parse file, delete the temporary file, and the move directly into insertion into whatever index system I develop for the hashing. While the former is more memory intensive, it does provide easier access for the threading part and would require less re-writing code. The only major issue that I see is that this code using the GEOS C++ API and I using the C API, which would require some conversion. I will most likely take the threading structure from this code and have it undergo a slight charge to use the C API.

The below command enabled C++17 as the default C++ version and also loaded C++20 which is great! Since all of the C++20 tools are now available to me, all of my concurrent options can stay within the standard library.

   scl enable devtoolset-11 bash

My goal for tomorrow is simple: use the code send to me to implement multi-threading for reading in the data. I think that each thread will separately return a GEOSGeometry* since in my final vision for the project the threads would directly continue into hash generation and insertion into the final data structure. To adapt this for the brute force case, a more complicated loop structure can be easily employed or copy the two sets of pointers into one contiguous array. After that, I need to return to the algorithmic side of things and the concepts from the literature review, a focus which I suspect will take at least a week.

Wednesday, 22 June 2022

Today I had one goal, to apply a multi-threading scheme to the functions to read in data for the brute-force Jaccard distance search, and I was successful. As both Dr. Puri and all of the friend who have used the C++ standard library threading capabilities have told me, that interface is clean and easy to use with any amount of concurrent background. All of the issues that I had with the threading part actually came from me misunderstanding the vector data structure and using the wrong functions to insert into it which caused me to try to join threads what weren’t actually threads or even initialized memory of any type (oops).

That brings me to the other think that I did today. This whole thing I’ve been working directly with pointers or double pointers for all of my data structures since those are the tools available in C which is what I am more familiar with. Well, C++ has this little thing called the standard library which has a lot of commonly used data structures like strings and vectors, which behave not unlike python’s lists. Take my read_wkt function. Since I cannot know how many polygons are in the file until I try to read them, a fixed length array cannot be used here so I originally malloced a GEOSGeomtry** pointer and then after inserting a new polygon into that I would have to check and realloc the array if needed. Well, vectors do all of that by default and are an overall more robust data structure. So, as part of rewriting the I/O code I adapted the WKT reading functions to use and output vectors since they are perfect for this purpose. I will be trying to use elements of the C++ standard library more often moving forward since they should produce more robust data structures and are likely optimized to a level that I do not have the time to do.

Today I also ran my brute force search through valgrind and patched several large memory leaks which were for even just 264 shapes leaking approximately 15 megabytes of memory. That had the potential to grow out of control very quickly as the size of the data set grew so I’m glad that I caught it now. All of the leaks were in code which I expect to use directly in my final solution, such as the Jaccard Distance function and polygon centering functions. Happily, valgrind is reporting that no leaks are possible for both the single threaded and multi-threaded variants of the brute force search. I am surprised that the program is allocating a total of 2.2 GB of memory, but I think that valgrind is reporting cumulative amount of memory allocated during the lifetime of the process, so the total usage at any given point should be substantially less since I tend to be zealous when it comes to freeing memory and not allocating too much.

I don’t have an exact goal for tomorrow, which is a bit unfortunate since I think that having such a clearly defined one today did help me stay focused and achieve measurable progress. I know that I need to return to some of the papers from the literature review and start designing the hashing process. I will probably focus on the below reference and in particular how their sketch technique is provably a LSH family.

M. Astefanoaei, P. Cesaretti, P. Katsikouli, M. Goswami, and R. Sarkar, “Multi-resolution sketches and locality sensitive hashing for fast trajectory processing,” in Proceedings of the 26th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Seattle Washington, Nov. 2018, pp. 279–288. doi: 10.1145/3274895.3274943.

Thursday, 24 June 2022

Today I transitioned back into looking at the theoretical properties and requirements of an LSH scheme for jaccard distance for polygons. I decided that I would start by trying to mirror the approach in [2], which is the traditional framework for LSH on text documents. However, even looking at [1] and [2] it became clear that the data I was using was different. Each element of the sketch that is produced following the idea of [1] falls in the range between 0 and 1 while the other two sources deal with discrete, generally binary data vectors. The very definition of the Jaccard similarity measure (and thus Jaccard distance) breaks down here. However, there are generalized definitions of Jaccard, which were discussed in [3]. These include the weighted Jaccard similarity, defined as

JaccardW(A, B) = (Σ_i min(A_i, B_i)) / (Σ_i max(A_i, B_i))

Please forgive the crudeness of that notation, this wiki has no ability to render proper math, but I generally followed LaTeX notation. This generalized definition works with vectors of positive weight, but it doesn’t handle vectors with different magnitude well. This is important because under my current sketching idea smaller polygons would intersect less disks and by nature have a smaller magnitude. Fortunately, while [3] presented the formula above, it was to serve as the benchmark for a new generalized definition of Jaccard which treats the vectors as probability distributions and thus the magnitude of the input vectors doesn’t matter. Their definition is below.

JaccardP(A, B) = Σ_{i : A_i B_i > 0} ((1) / (Σ_j max(A_j / A_i, B_j, A_i)))

Once again, I apologize for the poor math notation. This version of the Jaccard Index was designed to operate much closer to a drop-in replacement for the traditional definition and despite looking like an O(n^2) algorithm, the authors of [3] give a sorting method which can reduce computational complexity to O(n log n) using something like merge sort or (in practice if not in theory) quick sort.

The questions that still remain can be summarized with two board strokes:

• How well does JaccardP and the given P-MinHash of [3] fair in ANN searches?
• The P-MinHash approach will preserve JaccardP between the sketches, but does that preserve the Jaccard distance or similarity (recall how closely these measures are coupled) of the original polygons? Or it is possible that it is transformed into something else?

[1] M. Astefanoaei, P. Cesaretti, P. Katsikouli, M. Goswami, and R. Sarkar, “Multi-resolution sketches and locality sensitive hashing for fast trajectory processing,” in Proceedings of the 26th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Seattle Washington, Nov. 2018, pp. 279–288. doi: 10.1145/3274895.3274943.

[2] J. Leskovec, A. Rajaraman, and J. D. Ullman, Mining of Massive Datasets, 2nd ed. [Online]. Available: http://infolab.stanford.edu/~ullman/mmds/book.pdf

[3] R. Moulton and Y. Jiang, “Maximally Consistent Sampling and the Jaccard Index of Probability Distributions,” in 2018 IEEE International Conference on Data Mining (ICDM), Nov. 2018, pp. 347–356. doi: 10.1109/ICDM.2018.00050.

Friday, 24 June 2022

Today I continued to work on building up a LSH scheme. I focused on alternative definitions of the Jaccard similarity measure. In order to use either of the definitions that I reported yesterday, it is important that their is a geometric interpretation. A way to show that what I’m doing with the sketches can be traced back to polygons on the plane. I believe that I have found one for the weighted Jaccard similarity. It involved changing the sketching procedure from randomly placed disks to a tessellation of squares. Then consider the numerator and denominator separately. Treating the numerator as a polygon itself, it represents the maximum possible intersection between the two polygon while still respecting the cell borders and not moving any of the mass of the polygon between cells. Likewise the denominator represents the smallest possible union that still respects the cell borders. Naturally the intersection within a cell can never exceed the area of the smaller polygon and likewise the union can never be smaller then the area of the larger polygon fragment.

Unfortunately I was unable to find such a representation for the probabilistic Jaccard similarity. The more that I think about it though, the less sure I am that it is the metric of choice. It is scale invariant, which I’m not entirely sure is a good thing. Is the same shape but smaller or larger still “the closest shape”? How important is scale to this work? I’m not sure, but that is something that I will have to make up my mind about before transitioning back to the programming side of things. If I can’t find a geometric interpretation I will be more hesitant to use it, but as the authors in [3] state, “We will even show empirically that in some circumstances, it is better for retrieving documents that are similar under JW than JW itself” so even if I can’t find a geometric explanation it still could yield better results.

I found two articles [2, 4] about referenced by [3] which can be used to create a more efficient hashing approach for dense data vectors, but I have not read them in detail yet since I do not know if the polygon sketches I will be generating will be dense enough to justify these methods. Given my current thoughts about which Jaccard similarity to use, reading [1] will be important since it is where the weighted Jaccard comes from. However, starting Monday I will be taking some time to prepare for the mini-presentations happening on Wednesday. Working on draft slides on Monday will ensure that I am able to get good feedback from Dr. Puri.

[1] O. Chum, J. Philbin, and A. Zisserman, “Near Duplicate Image Detection: min-Hash and tf-idf Weighting,” in Procedings of the British Machine Vision Conference 2008, Leeds, 2008, p. 50.1-50.10. doi: 10.5244/C.22.50.

[2] C. J. Maddison, D. Tarlow, and T. Minka, “A* Sampling,” in Advances in Neural Information Processing Systems, 2014, vol. 27. Accessed: Jun. 24, 2022. [Online]. Available: https://proceedings.neurips.cc/paper/2014/hash/309fee4e541e51de2e41f21bebb342aa-Abstract.html

[3] R. Moulton and Y. Jiang, “Maximally Consistent Sampling and the Jaccard Index of Probability Distributions,” in 2018 IEEE International Conference on Data Mining (ICDM), Nov. 2018, pp. 347–356. doi: 10.1109/ICDM.2018.00050.

[4] A. Shrivastava, “Simple and Efficient Weighted Minwise Hashing,” in Advances in Neural Information Processing Systems, 2016, vol. 29. Accessed: Jun. 24, 2022. [Online]. Available: https://proceedings.neurips.cc/paper/2016/hash/c2626d850c80ea07e7511bbae4c76f4b-Abstract.html

Week 5

Monday, 27 June 2022

Today started with a lecture lead by Dr. Brylow about giving good research talks. This was somewhat amusing since he was both late and didn’t finish his slides for the talk. Afterwards, I created a draft of the slides for my 10 minute mini-presentation on Wednesday. I will be discussing it with Dr. Puri tomorrow, but I hope that I did a good job distilling my work into a handful of slides. Some of the feedback I got from our presentations in my Data Mining class suggests that I often take a more technical approach that desired…

After drafting those slides I continued work on finding geometric meaning for the probabilistic Jaccard similarity. This time I noticed a different definition which directly related to JW, which was easier to interpret. Take a generalized definition of JW:

JW(x, y, a) = Σ_i [ min(a_i x_i, y_i) / (Σ_j max(a_i x_j, y_j)) ]

JP happens to occur when a_i x_i = y_i which is what makes it scale invariant. Then, we can observe that the denominator becomes the minimum area of the union of the scaled polygon X and polygon Y using similar logic to the above post. I will admit that I’m not entirely sure how to interpret this but it seems clear that it doesn’t have the same clear geometric interpretation that JW has and probably doesn’t accurately preserve the Jaccard similarity of the original polygons. That doesn’t prohibit it from being useful in the future but I can’t afford to spend too much time on it right now. I’m doing to work on it tomorrow, but after that I can’t delay continuing development of the rest of the LSH scheme. This is a problem that I could always come back to, time permitting.

Tuesday, 28 June 2022

After three days of though, I believe that I have a geometric interpretation of JP, but I’m not going to go into too much detail since I also decided that JW makes more sense, at least for now, since it does accurately preserve the Jaccard similarity of the original polygons. Time permitting, I would be interesting in dropping JP into an LSH implementation using JW just to see how well it works.

I read the below paper:

O. Chum, J. Philbin, and A. Zisserman, “Near Duplicate Image Detection: min-Hash and tf-idf Weighting,” in Procedings of the British Machine Vision Conference 2008, Leeds, 2008, p. 50.1-50.10. doi: 10.5244/C.22.50.

This paper didn’t actually teach me a lot. It seemed lighter than I would have expected on technical details and revisited the traditional minHashing algorithm used in text mining. While it does proved some intuitive definitions for two variants of the Jaccard index, these are based mostly on sets and weighted sets while only loosely translate to the geometries that I am considering.

I also started, but did not get a chance to finish this paper, but it seems very promising. It’s not everyday that a paper claims to get a 60,000 time speed up over that previous best method using JW.

A. Shrivastava, “Simple and Efficient Weighted Minwise Hashing,” in Advances in Neural Information Processing Systems, 2016, vol. 29. Accessed: Jun. 24, 2022. [Online]. Available: https://proceedings.neurips.cc/paper/2016/hash/c2626d850c80ea07e7511bbae4c76f4b-Abstract.html

Finally, I revisited my slides for the presentation tomorrow with a suggestion from Dr. Puri and based on the methodology I was describing to him, he recommended another paper which I will have to read at some point.

L. G. Azevedo, G. Zimbrão, J. M. de Souza, and R. H. Güting, “Estimating the Overlapping Area of Polygon Join,” Berlin, Heidelberg, 2005, pp. 91–108. doi: 10.1007/11535331_6.

Wednesday, 29 June 2022

Much of today was taken up with the mini-presentations and some late minute prep and slide tweak that I made for it.

I did finish the paper from yesterday which was fascinating since that I had actually thought of some of the underlying principles of this paper. Some of the critical differences are that they fixed the start of each of the intervals for each element and returned the number of random numbers needed to find a valid sample. This hashing scheme will likely be the one that I use, but it is sensitive to the sparsity of the data. Specifically, we want dimensions that are frequently somewhat busy and we do not want dimensions which are rarely used since any random number within the range of that element will cause a rejected sample. A possible solution here is to count the number of polygons which are present in a cell over the whole dataset and drop those which are not used too much.

A. Shrivastava, “Simple and Efficient Weighted Minwise Hashing,” in Advances in Neural Information Processing Systems, 2016, vol. 29. Accessed: Jun. 24, 2022. [Online]. Available: https://proceedings.neurips.cc/paper/2016/hash/c2626d850c80ea07e7511bbae4c76f4b-Abstract.html

After that I started thinking about the rest of the LSH process. I think that the most naive approach would be to directly using a hash table. We want to create a table such that each hash has one bucket and use chaining within the bucket which would be the set of polygons with the same hash. Linear probing would have to be used to ensure that each bucket only has one hash value in it.

Despite a lot of research papers about generating these hashes, it does seem that there is significantly less work on the data structures used to store and retrieve then, although tomorrow I will be reviewing the papers that I have read that detail their data storage schemes.

Thursday, 30 June 2022

Today I continued working on the rest of the LSH scheme, focusing on how the hash tables are structured to prove reasonable lookup time and space complexities. I was originally thinking of one primary hash table where each bucket corresponded to one LSH hash and possibly a second hash table storing the final cell location of each LSH hash value after linear probing since chaining is not really an option here; we cannot have dissimilar LSH hashes in the same bucket. After thinking about this for the morning, I started reviewing the data structure schemes used in other papers that I had already read. One of my primary sources early on, “Multi-resolution sketches and locality sensitive hashing for fast trajectory processing” did detail a data structure but they focused on the connections between layers without detailing how each layer worked. When I checked “Accelerated similarity searching and clustering of large compound sets by geometric embedding and locality sensitive hashing” they referred in completely different data structure which had it’s own research paper focused excursively on the structure and query operations for LSH, cited below.

1. Q. Lv, W. Josephson, Z. Wang, M. Charikar, and K. Li, “Multi-probe LSH: efficient indexing for high-dimensional similarity search,” in Proceedings of the 33rd international conference on Very large data bases, Vienna, Austria, Sep. 2007, pp. 950–961.

This was excellent. It gave an overview of the basic LSH hashing scheme developed in [2] which highlighted some misunderstandings that I had particularly about the number of hash tables involved before detailing a new process for querying LSH tables which provided a 10 - 15 times space reduction with similar time complexity and other properties compared to the basic LSH scheme. For more information on the basic scheme, they referenced a paper which I had already read but doesn’t do a whole lot with hash tables and the below citation.

2. A. Gionis, P. Indyk, and R. Motwani, “Similarity Search in High Dimensions via Hashing,” in Proceedings of the 25th International Conference on Very Large Data Bases, San Francisco, CA, USA, Sep. 1999, pp. 518–529.

I have not had a chance to read that paper, but since the multi-probe scheme offers massive space complexity improvements without other performance sacrifices I will focus on that paper for the time being. They had an assumption about the type of hash function uses, naming that it can be expressed as

h_a,b(v) = ⌊a*v +b / W ⌋

For some real valued vectors a and b. This is many surface level similarities with the hashing proposed in “Simple and Efficient Weighted Minwise Hashing” so I suspect that the two methods will play nicely together. However, I don’t intend to leave that to chance so my goal for tomorrow is to compare the hash generation technique with the hash storage and retrieval operations to ensure that they are compatible. Looking forward into next week, I need to clean up the notation and formalize my notes on the processes as I begin to prepare to transition back into programming towards the end of week six. Ideally this will also have pseudocode as part of that process but detailed, step-by-step algorithmic instructions will also but sufficient. After implementing those algorithms, I will have to design some performance tests to see how the system performs.

Friday, 01 July 2022

So, one of the things that makes the Multi-probe LSH so efficient is the ability to do query-directed probing sequences. In order to facilitate this an understanding is needed of the probability that a similar point to the query point would produce a given perturbed hash. The original multi-probe LSH paper uses Euclidean based hashed functions which project a vector unto a line and return which “slot” on the line that the projected vector falls into. Their critical observation was that if a query point q was mapped close to one of the boundaries of the slot, it was much more likely that a similar point could be found just over that boundary rather then in the cell adjacency to the far boundary. This in turn creates a normal distribution and can be used to score perturbation vectors and enable the query-directed probing sequence. However, the weighted Jaccard hashing that I would like to use has different properties. It returns the number of hashing attempts before a successful one was found. Mapping these values into the same notion of buckets means that we need a way to find the probability that a different hash would result from a similar point. This seems like an important property so I turned first to the literature to find if anybody has implemented Multi-probe LSH with Jaccard and found… nothing. As far as I can tell, multi-probe LSH has been used with Euclidean distance and cosine similarity but nobody has used it with Jaccard similarity or distance. This was based off of my know search and a short paper put out by the authors of the original multi-probe LSH paper which summarized the work that has been done since (although that was originally published in 2017 and could be out of date itself by now).

As far as I can tell, finding an efficient way to estimate the probability that nearby hashes have similar points to a query would be a new and significance contribution to the existing LSH literature. For the sake of completeness, here are some of the relevant papers, but I have read the abstract for many more today which proved to be not relevant to this problem.

1. Q. Lv, W. Josephson, Z. Wang, M. Charikar, and K. Li, “Multi-probe LSH: efficient indexing for high-dimensional similarity search,” in Proceedings of the 33rd international conference on Very large data bases, Vienna, Austria, Sep. 2007, pp. 950–961.
2. Q. Lv, W. Josephson, Z. Wang, M. Charikar, and K. Li, “Intelligent probing for locality sensitive hashing: multi-probe LSH and beyond,” Proc. VLDB Endow., vol. 10, no. 12, pp. 2021–2024, Aug. 2017, doi: 10.14778/3137765.3137836.
3. A. Shrivastava, “Simple and Efficient Weighted Minwise Hashing,” in Advances in Neural Information Processing Systems, 2016, vol. 29. Accessed: Jun. 24, 2022. [Online]. Available: https://proceedings.neurips.cc/paper/2016/hash/c2626d850c80ea07e7511bbae4c76f4b-Abstract.html
4. S. Liu, J. Sun, Z. Liu, X. Peng, and S. Liu, “Query-Directed Probing LSH for Cosine Similarity,” in Proceedings of the Fifth International Conference on Network, Communication and Computing - ICNCC ’16, Kyoto, Japan, 2016, pp. 171–177. doi: 10.1145/3033288.3033318.

Week 6

Monday, 04 July 2022

Today was spend working on creating a success probability estimation for the weighted Jaccard index and while progress wasn't too fast, it was made. Given the lack of good math notation on the wiki, I will not dive too deeply into these definitions. However, I believe that the weighted hashes can be modeled as a negative binomial distribution were we conduct trails until a "success" (or failure depending on your view) of landing a random number in the green region is found. The formula given in "Simple and Efficient Weighted Minwise Hashing" align with the expected value and variance given on the wikipedia definition for the negative binomial distribution. This happens with a probability equal to the effective sparsity of the vector we are hashing, which is the area of the green region over the total region. The probability of each hash value for some query vector q equals (1 - sq) to the h(q) power where sq is the sparsity of q and h(q) is the hash value of interest.

I believe that working the the probability of some point p having a hash value of h(q) + δ for some δ in {-1, +1} can be measured by the sum of h(q) + δ for all values of delta. However, this seems to have a property that I was not expecting. This always values hashes with lower values since the effective sparsity is always less than 1. That means that it thinking that a hash value of 1 is always the most likely even when the expected value of the hash is 1 / sq and follows standard binomial properties. This tracks with a negative binomial distribution with r = 1 but still something feels off about it that I just can't seem to put my finger on. So even if the expected value is greater than the value of h(q), minimizing the sum of h(q) + δi across i will prioritize subtracting one from h(q) since it leads to a higher probability density function than moving it towards the expected value. That being said, I most likely need to adjust the working formula to move towards the expected value at all times and the reason why this isn't a problem for the Gaussian version in the multi-probe LSH paper is because the densest point of the pdf is the expected value, i.e. the peak of the bell curve.

This is what I will be working on tomorrow but after that I believe that I will be ready to start construction on the multi-threading parts of the data structures. If I learned anything in concurrent computing it was that having a plan before starting a multi-threaded project will save a lot of work in the long run.

Tuesday, 05 July 2022

I continued to work on connecting the weighted Jaccard hashing with the multiprobe LSH querying procedure. In the process I completely re-wrote everything that I had done last night but still wasn't able to find anything promising. Everything seemed to just come down to 'sum the elements of the perturbation vector' which prioritizes vectors summing to zero even when the magnitude of the individual elements is way too large to be useful over vectors which sum to say plus or minus 1 and actually contain near neighbors to the query.

During my meeting with Dr. Puri, we decided to stop working on the multiprobe side of things. It would be an awesome improvement to any LSH scheme I develop, but at the end of the day it is exactly that; an improvement that is not required to get an operational system finished. This was a good decision and discussion since I will fully admit to having a problem with attempting to do the most complex and intensive version of the work as possible, almost always to my detriment. The analogy here, I suppose, is the difference between creating a new puzzle piece or connecting existing ones in a way that nobody else has done. I'm convinced that this is possible, however I certainly don't have the time for it this summer and likely don't have the required background working with all of these statistical distributions.

So, moving forward I will focus on the traditional LSH query scheme, which is basically to have generated a number of different hashes for the same object and linearly scan the union of the bucket of the query object in each hash table. Below is the citation for the paper which I believe was the first to detail this hashing scheme:

1. A. Gionis, P. Indyk, and R. Motwani, “Similarity Search in High Dimensions via Hashing,” in Proceedings of the 25th International Conference on Very Large Data Bases, San Francisco, CA, USA, Sep. 1999, pp. 518–529.

I also need to read a paper which Dr. Puri send me a while ago which has some very similar ideas about polygon sketches apparently.

1. L. G. Azevedo, G. Zimbrão, J. M. de Souza, and R. H. Güting, “Estimating the Overlapping Area of Polygon Join,” Berlin, Heidelberg, 2005, pp. 91–108. doi: 10.1007/11535331₆.

After this reading, I will find the synchronization requirements of the system so that I am can implement the system with multi-threading in mind, even though I will start with a single threaded approximate search on the very small data set that I have been working with so far. The advantage here is that I can use the brute force as a ground truth to check things like the accuracy and recall of the new model. After proving the principles on the tiny data set I will repeat the process with a larger set but still small enough that a ground truth can be found via brute-force methods.

In facts, lets set some dates for these accomplishments:

1. 08 July 2022, Finish data structure planning and enumeration of synchronization requirements.
2. 15 July 2022, Initial implementation of hashing algorithm and LSH hash tables.
3. 22 July 2022, Multi-threaded implementation of hashing algorithm and hash tables.
4. 27 July 2022, Develop testing framework and metric.
5. 29 July 2022, Finish performance tests.
6. 05 August 2022, Final paper is due.

This seems like a very short amount of time now that I have put dates on it. The multiprobe side of things will have to wait for some future work since it seems clear that I will not have time for it now.